Let me ask you a question, have you ever used the Measurement Uncertainty (MU) reported in your calibration certificate?

Most users of certificates that I meet who are In-charge in calibration do not use the measurement uncertainty results in their calibration report. It is either they do not really need it or do not understand its use and importance. 

When I was a calibration technician that does not understand the use of measurement uncertainty, I felt incomplete and incompetent as a calibration technician.

Every time I see a calibration certificate with MU results, I ignore it and move on to other results. There is no meaning for me because I do not understand its importance.

One of the essential knowledge in interpreting a calibration report is to understand the measurement uncertainty results with it. As a calibration technician, understanding the use of MU should be one priority to be learned.

These are the questions that always came into my mind back then. Through continuous learning, I found the answers which I will share with you in this post.

1. We always read or heard that MU is the quantification of the measurement doubt, but how does it quantify?
2. How is Measurement uncertainty related to the traceability chain?
3. Why should you not perform a calibration if you do not know the measurement uncertainty of the calibrator? 

To see the importance of Measurement uncertainty reported in a calibration certificate, I will present 8 ways on how to use measurement uncertainty. 

These are:

1. Used to determine the ” Range of True Value” (True Value)
2. Measurement Uncertainty Provides Meaningful Comparison of Measurement Results.
3. Used to Calculate TUR (Test Uncertainty Ratio)
4. Used as a Tolerance Limit
5. Providing Confidence and Traceability Evidence For the Unbroken Chain of Calibration
6. For Conformity Assessment, An Important Element for a Decision Rule
7. One of the Main and Important Components in Measurement Uncertainty Calculation
8. Used to determine performance  for Proficiency Test (PT) or Inter-laboratory Comparison (ILC) 

Once you understand how to use it, you will then appreciate its importance (I hope), then your confidence in interpreting the calibration results in a certificate will also increase. So let us start.

Now, let us see a simple measurement uncertainty definition that I read so far which is non-technical.

What is Measurement Uncertainty?

Measurement uncertainty is the quantification of doubt that exists in a measured value. 

Since there are no exact measurement results, there is always that doubt with it, an uncertainty. 

And to determine the numerical value of that doubt is to perform measurement uncertainty calculation. This means that doubt in measurements can have a value or exact number to present it. 

To explain further, I will define measurement uncertainty in the below figure.

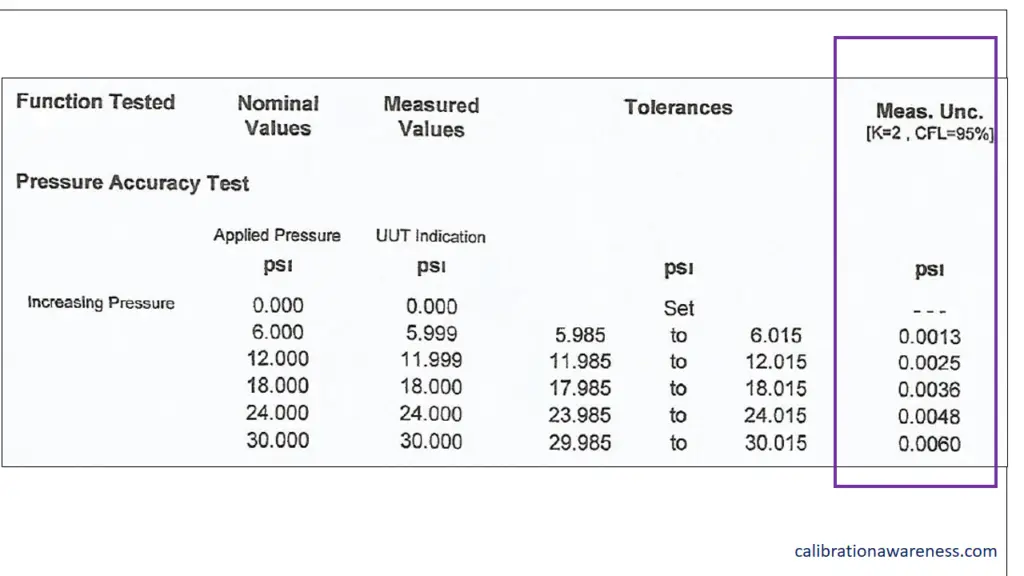
We should always use the complete measurement results or range of true values.

For example (refer to Figure 1 below), if you see measurement results that read like this: 500+/-3.9 psi, this means that it is not sure that the exact value is 500, this is the doubt, but we are sure that the true value is within the range 496.1 to 503.9 psi – this is the quantification of the doubt.

We should always use the complete measurement results or range of true values.

To explain further, see Figure No. 1 below.

Having this knowledge in understanding measurement uncertainty will lead us to the 8 important ways to use a MU in our measurement decision process.

8 Important Uses of Measurement Uncertainty Reported in a Calibration Certificate

1. Used to determine the ”Range of True Value” (True Value)

This is the main and the simplest use of measurement uncertainty, to determine the true value of measurement results. 

With the knowledge of true value, you can determine:

1. Decision rule implementation in conformity assessment to determine a pass or fail decision – see no 4
2. Meaningful comparison of measurement results to see what is appropriate to use- see no 2 below

True value can be calculated by simply using the MU same as we use a tolerance limit. To add and subtract to the measured value.

Take note that the exact true value does not exist, therefore, it is also called a “range of true values”. It is also known as a “complete statement of results”. See below photo

The doubt that exists in a measured value is the measurement uncertainty interval, this is the quantified value of the doubt. Based on the above photo, the quantified value of doubt is from 496.1 to 503.9. 

Therefore, the smaller the MU, the lesser the doubt, the greater the confidence that the measured value is really the True Value (TV)

2. Measurement Uncertainty Provides Meaningful Comparison of Measurement Results.

Measurement Uncertainty (MU) gives more meaning when deciding the best measurement results. When accounting with MU in our MV, we are using the True Value or the “complete statement of result” as our guide when making comparisons of measurement results.

It helps us compare two measurement results that show which one is really the most acceptable or appropriate to be used.

To explain clearly, observe the chart below:

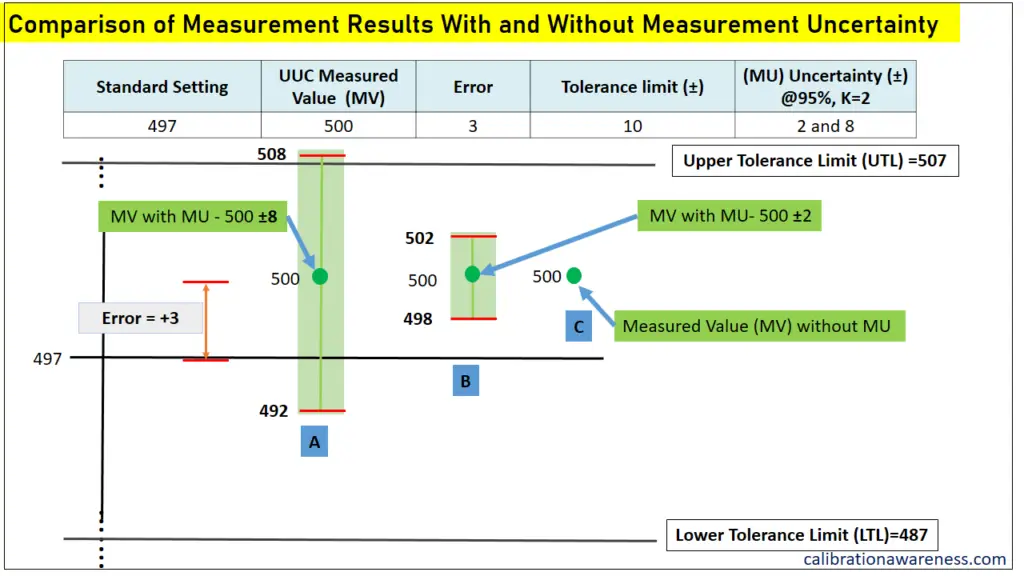
Based on Figure 2 above, you can observe 3 cases representing the measured value.

Without considering measurement uncertainty, cases A, B, and C have the same interpretations.

Looking at case C alone, where only the measured value is given, it is hard to make a comparison and therefore, a decision. 

 But once we account for the measurement uncertainty, we can now observe a big difference. There is now ‘quality’ that is set for comparison.

If we compare A and B results, even though they both have the same Measured Value, once we account for the measurement uncertainty, it is obvious now that case B has the best performance since it has a smaller MU. The confidence that the true value stays in-tolerance is higher.

In case A, where measurement uncertainty is larger, it is a probability that it is already out-of-tolerance, thus, confidence is smaller.

The point in this comparison is that, if you want much higher confidence and the probability that the MV with MU (True Value) stays in-tolerance, choose a reference standard with smaller uncertainty or with a higher TUR.

3. Used to Calculate TUR (Test Uncertainty Ratio)

What is a TUR (Test Uncertainty Ratio)?

One important use of MU is to calculate TUR  or Test Uncertainty Ratio. Based on the comparison above, a higher TUR is better than a lower TUR.

As per the definition, TUR is the ratio between the Tolerance of the UUC and the Expanded Uncertainty of the calibration process. I believe you are familiar with the ratio of 4:1. This is the recommended TUR  by known publications and guides. 

Please do not be confused with TAR or Test Accuracy Ratio which is the old term.

Why do we need to calculate TUR?

Before we perform any calibration, it is a requirement to use appropriate reference standards. Appropriate means that the reference standard should be more accurate than the UUC.

We need TUR to compare the accuracy of the UUC against the measurement uncertainty value of the reference standard (combined with other contributors).

This will inform you how good the performance of the calibration performed in a specific UUC as per the reference standard used. In simple terms, high TUR means a high accuracy rating of the reference standard used for calibration.

Like for example, if you follow the 4:1 requirement, the reference standard to be used should be 4 times more accurate than the UUT to be calibrated. 

To determine this relationship, we need to calculate the TUR.

How to Calculate TUR

The formula to calculate a TUR:  see below photo

Remember that the Measurement uncertainty used is from the measurement uncertainty value of the calibration process which can be seen in the calibration certificate of the calibrated UUT.

4. For Conformity Assessment – An Important Element for a Decision Rule

When we say conformity assessment, there is a ‘passed or failed’ decision with it. It is part of our verification process to determine conformance to specifications.

In order to determine a pass or failed decision, there is what we call a “decision rule” to be followed. 

As per ISO 17025, a decision rule is a rule for conformity assessment that accounts for the measurement uncertainty in the measured value before deciding. See the below photo where measurement uncertainty is accounted for before stating conformity.

Therefore, we cannot meet the requirements of ISO 17025 about decision rules if we do not have a measurement uncertainty that results in our measured value during conformity assessment.

Check out my other post in this link for more explanation about Decision Rule

5. Used as a Tolerance Limit

Sometimes, we do not know the tolerance limit of a specific UUC, and sometimes even the manufacturer does not provide it.

One solution is to use the measurement uncertainty reported in its calibration certificate. 

Since measurement uncertainty is the combination of all the valid sources of errors that are statistically calculated, we can use this as our tolerance limit. 

This is comparable to the limits of a control chart where 2 sigma and 3 sigma are used as a control limit. Measurement uncertainty is reported with k=2 or 2 sigma.

Sometimes or most of the time, MU values are very small which makes it very strict if you use it as a tolerance limit. What you can do is multiply it by 2 to expand it to a 99% confidence level (3 sigma).

Note, that this is just my recommendation, you need to document this method and have it approved before implementing it.

6. Providing Confidence and Traceability Evidence For the Unbroken Chain of Calibration

We always read in the calibration certificate the statement “the calibration performed are traceable to International Standard through….”

But how do you know it is really traceable to International Standards?

First, let us define Traceability or Metrological Traceability and traceability chain.

Metrological Traceability (VIM3 clause 2.41): Property of a measurement result

whereby the result can be related to a reference through a documented unbroken chain of

calibrations, each contributing to the measurement uncertainty.

Metrological Traceability Chain (VIM3 clause 2.42): Sequence of measurement

standards and calibrations that are used to relate a measurement result to a reference.

Measurement Uncertainty results represent the documented “unbroken chain of calibration”. It is the traceability chain that links one measurement standard to another in decreasing sequence starting from the top (or increasing if starting from the bottom). See the below photo.. 

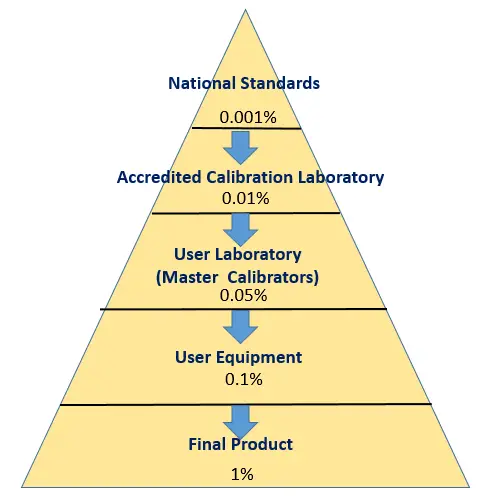
Measurement Uncertainty results are the objective evidence of the “unbroken chain of calibration” performed.

If you cut this chain (by using a calibrator without measurement uncertainty coming from higher recognized laboratories), it means it is not a traceable calibration, and the succeeding calibrations that you will perform using the same calibrator.

You should verify the calibration certificate of your master standard after calibration for measurement uncertainty results to ensure the continuation of the traceability chain and therefore maintain traceability in calibration and confidence in measurements.

When we use the calibrated instrument as a master calibrator, we will use also its MU value to calculate the MU of the next UUC, thus establishing the next traceability chain. See no 7 below.

To read more about traceability, visit my related post in this link >> The Deeper Meaning of a Traceable Calibration Every Calibration Technician Must Understand

7. One of the Main and Important Components in Measurement Uncertainty Calculation

Measurement uncertainty itself is also one of the major contributors to uncertainty in measurement. 

This is why there is no such thing as exact measurements because of this uncertainty in measurements even if it is the master standard. 

Remember the Measurement traceability chain where each standard has its uncertainty contribution linking every standard in a chain.

We will consider measurement uncertainty results from the calibration certificate under the Type B uncertainty contribution added to the uncertainty budget. 

An uncertainty budget is a form of a table that summarizes and tracks all the valid uncertainty contributions. It will also make the calculation simple and organized like in the Excel worksheet. See the below example of an uncertainty budget.

This also applies during CMC calculation for the laboratory scope.

8. Used to Determine Performance in Proficiency Test (PT) or Inter-laboratory Comparison (ILC)

Last but not least,  Measurement Uncertainty is used to calculate the performance of measurement results during PT(Proficiency Test) or ILC (Inter-laboratory Comparison)

PT or ILC is an activity for quality control.  It is used to validate a specific procedure, method, or measurement process by comparing the results to other laboratories.

One of the formulas used to evaluate PT/ILC results is the En Ratio or En Number. 

En Ratio includes Measurement Uncertainty results in its formula. With this formula, you can determine if the PT or ILC performed has passed or failed. Refer to the below photo.

Performance Criteria:

• When the value of En is between -1 and +1, the results are considered satisfactory.

• When the value of En <-1 and En>+1, the results are considered unsatisfactory.

If you are applying for accreditation, PT/ILC it is a mandatory activity required by the accreditation body

With all these advantages of using measurement uncertainty, now the question is, do you know how to calculate Measurement Uncertainty? 

Conclusion

Measurement uncertainty is one of the most important elements in calibration. Without measurement uncertainty, we cannot say that we have performed a complete calibration.

Measurement Uncertainty is one of the neglected results that need interpretation in a calibration report. To appreciate and learn to interpret it, we need first to understand how it is being used.

In this post, I have explained what is Measurement Uncertainty and presented 8 different ways on how to use it during your measurement process. These are:

1. Used to determine the ” Range of True Value” (True Value)
2. Measurement Uncertainty Provides Meaningful Comparison of Measurement Results.
3. Used to Calculate TUR (Test Uncertainty Ratio)
4. Used as a Tolerance Limit
5. Providing Confidence and Traceability Evidence For the Unbroken Chain of Calibration
6. For Conformity Assessment – An Important Element for a Decision Rule
7. One of the Main and Important Components in Measurement Uncertainty Calculation
8. Used to determine performance for Proficiency Test (PT) or Inter-laboratory Comparison (ILC) 

I hope this post has boosted your knowledge and confidence to use and interpret the MU results reflected in your calibration certificate.

Do you have other uses for your MU reported in your calibration report? Please comment below.

Do not forget to subscribe!

Connect with me on my Facebook page.

Best Regards,

Edwin