Have you encountered the following scenario?

You are interpreting a calibration certificate but you noticed that the correction factor you need is not exactly displayed or provided in the report, what can you do?

The measurement data of your instrument based on the calibration results have errors. There are chances that specific measuring instruments cannot be adjusted. It is either not included in the design or simply not adjustable physically or automatically. Again, what can you do?

The question above can be answered by using a technique wherein we can adjust a measured value by simply determining what we call a “correction factor”.

One of the important skills for a calibration technician to have is to learn how to use the correction factor in a calibration certificate. 

This method is important when reviewing or interpreting a calibration certificate. A simple technique that we must learn to improve our measurement results and in effect improve our process.

In this post, I will share with you the following:

1. What is a Correction Factor in Calibration?
2. Important Use of a Correction Factor in Measurements
3. 4 ways to Apply Correction Factors In a Calibration Certificate
   • Applying the “Correction” value directly
   • Using the Nearest Reported Correction Value in the Certificate
   • Averaging Between 2 Correction Factors
   • Linear Interpolation to Determine Any Value Between 2 points
4. Example of How to Apply the Correction Factor

First of all, let us define the meaning of a Correction Factor.

What is a Correction Factor in Calibration?

Definition of a Correction Based on VIM 2.53,

Correction – compensation for an estimated systematic effect

Correction Factor (CF) is a value that we either add or subtract to compensate for the error from a systematic effect. This correction factor is based on “Correction” from a calibration result calculated using the equation:

.

From the statement that “ No measurement is perfect“, the correction factor is also just an estimate even though we see it as an exact value of the compensated error (systematic error).

There are other ways to compensate for an error but this is the simplest when it comes to the reported results in a calibration certificate.

Correction Factor is sometimes known as “corrective factor” and “calibration correction“

Why do we need to calculate the correction factor?

“You cannot perform adjustment if you do not know the corrections you need to apply”

One very important reason we perform calibration is to determine the error and at the same time, the corrections to correct the error afterward.

Errors can only be detected by performing calibrations. But once an error is detected, we should do something about it. It is either we adjust (using the provided zero and span error adjustment) or perform a correction factor if we cannot adjust it.

If there is a ‘correction factor and you do not know how to apply it, then you did not fully use the actual application of calibration, therefore calibration results become useless in our process application.

If you want the best results from a calibration result, then you need to learn the technique of determining the proper correction factor.

This is one reason we need to review the calibration or measurement results from a calibration certificate– to determine if we need a correction before we can use the value from the calibration result.

Another reason why we need to calculate or use a correction factor is to ensure that we meet the specified requirements of our calibrated reference standards or reference materials. We need to ensure that we use an updated correction factor every time a recalibration or new calibration takes place. This is a requirement under clause 6.4.11 of ISO 17025:2017 which states that “When calibration and reference material data include reference values or correction factors, the laboratory shall ensure the reference values and correction factors are updated and implemented, as appropriate, to meet specified requirements.”

Important Use of a Correction Factor in Measurements

Correction Factors compensate for the error that we encounter during calibration. The following are some of the important reasons why we need to use the Correction Factor, these are:

1. To make a measurement closer to the true value.
2. To adjust a measurement value that cannot be adjusted physically or by any software
3. To return equipment performance to a tolerable result or to a more accurate condition closer to the standard value
4. To reduce the effect of a systematic error.

What are these Systematic Errors that we need to correct?

Systematic errors are the errors that are known or unknown to us, known errors can be corrected or compensated. It is a consistent deviation in measurement. These systematic errors are from:

1. Measurement procedure -Positioning or setup and execution of methods during calibration
2. Effect of environmental conditions– Instruments operating in harsh or variable environments may experience systematic errors due to external factors such as electromagnetic interference, humidity, or pressure.
3. Personal error due to habits or improper training of the observer
4. Errors directly from instruments or the ‘Bias’– uncorrected errors from calibration standards can introduce systematic errors. Regular verification and recalibration of standards can help address this issue.
5. Instrument error from improper calibration
6. Zero Error – occurs when the instrument’s reading is not zero when the input or measurement signal is zero.

In every correction that we perform, remember that this is not also perfect, measurement uncertainty still exists, therefore, measurement uncertainty should still be considered.

4 Ways to Apply Correction Factors (CF) In a Calibration Certificate

Below are the techniques used on how to calculate correction factors in a calibration result that you can use.

1. Direct application using the Correction value
2. Using the Nearest Reported Correction Value in the Certificate
3. Averaging Between 2 Correction Factors
4. Using Linear Interpolation to Determine Any Value Between 2 Points

There are other methods and correction factor formulas out there but these 4 are the simplest and the only method I use as per my experience.

1. Direct Application using the “Correction” Value

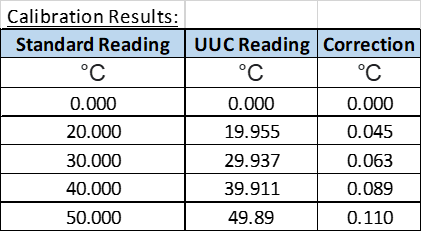
The Correction Factor formula for calibration is:

Correction = (True Value) – (Measured Value)

Correction = Correction Factor (CF)

     CF = – Error

Example above @20 °C range:

Correction = 20.000 – 19.955 = 0.045 °C

CF = 0.045 °C

2. Using the Nearest Reported Correction Value in the Certificate

This is the technique that I can say is based on common sense to determine the correction factor.

You can apply this technique if a small difference does not have a significant impact on the results, or it is negligible because of a wide tolerance limit or the effect of resolution (low-resolution instrument), then this is a quick way to determine and estimate the correction factor.

If the measured value you need is not in the middle but very close to either the upper or lower range, just choose the one where it is closer.

See the below example.

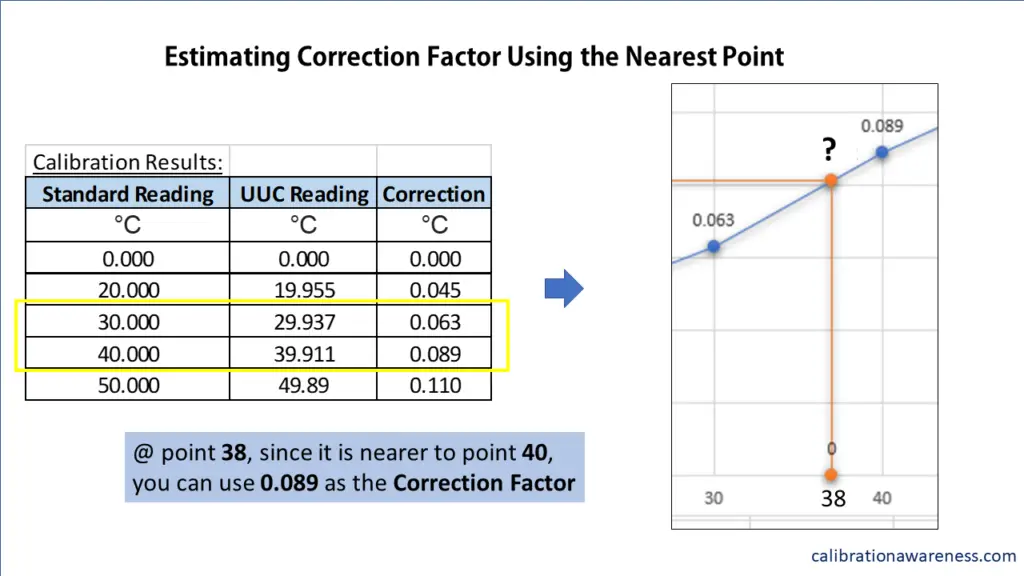
How to Determine the correction factor if the exact value you need is not given? Or, how to adjust the correction factor to have the exact value you need?

To answer these, let us discuss the next 2 techniques, read more below…

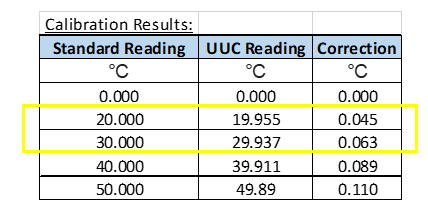
3. Averaging Between 2 Correction Factors

If you only need to calculate the value of a correction factor between 2 successive points, you can use the Averaging Method. Just add the 2 successive points then divide it by 2. See the below example using the same data points above:

For example, we need the CF of the value equal to 25

The values that we need are the Correction Factor between 20 and 30 which are equal to 

0.045 and 0.063. 

Now we can calculate the CF for Standard Reading at 25

CF = [(0.045)+(0.063)]/2

CF= 0.0108/2

CF = 0.054

4. Using Linear Interpolation to Determine Any Value Between 2 Points

If 2 points are given (which are the Max and Min points) with Correction value in an increasing (or decreasing) manner, we can calculate any value in between using Linear Interpolation.

Linear Interpolation is best used when we want to determine the value that lies anywhere in a given range bounded by Max and Min points.

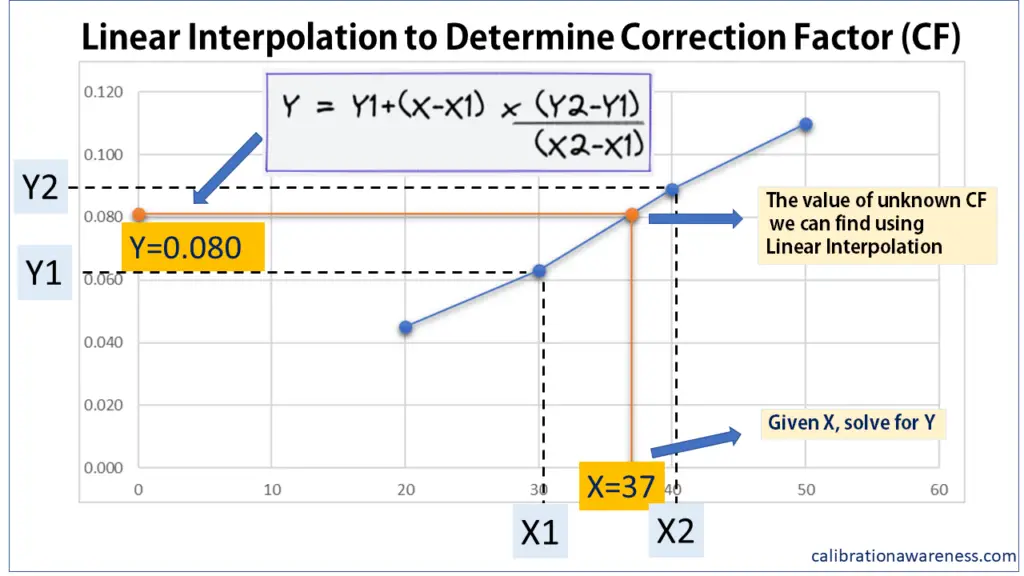
The equation for a linear Interpolation is:

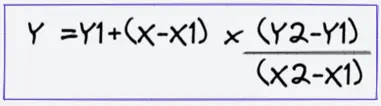
Where:

X1 and X2 are the given Standard Readings

Y1 and Y2 are the equivalent Correction Factors (or correction value)

X =The required standard value where Correction Factor is needed

Y = the calculated Correction Factor based on X

For example, determine the Correction factor @ point 37 in the table below (You can refer to the graph above):

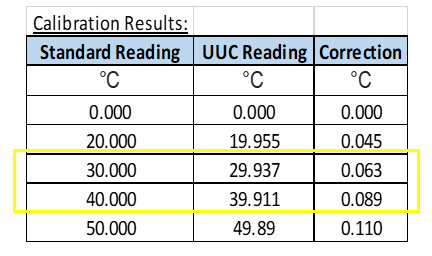
Solution:

Example of How to Apply the Correction Factor

Given below calibration results of a balance: (example only)

During the review of the calibration results, you notice that the balance is not adjusted but a “correction” was provided. See table above.

When you see a result like this, before you use the actual value of the balance, use the correction value, which is now the “correction factor” that will compensate for the error.

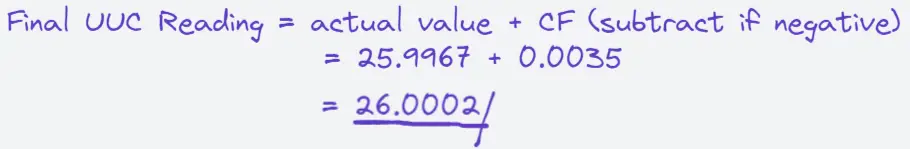
The “Final UUC Reading” will become now your final value to be applied during your measurement process.

In this way ERROR is now compensated (ERROR =0), our actual value will now equal to the Standard value, therefore, accuracy was increased.

Remember that the Correction factor is the result during calibration which is used to offset the error and therefore should be subtracted (or added) on the final value of the balance (UUC) results. A correction factor is applied to all instruments that cannot be adjusted, that is why we calculate the correction factor manually.

Conclusion

One of the most important skills when interpreting and using a calibration result is the capability to understand and calculate Correction Factors. One good reason is for us to appreciate more the importance of a calibration result by achieving the most accurate measurements.

Correction Factor helps us achieve more accurate measurement results by simply compensating for the error.

Correction factor is also known as calibration correction and/or corrective factors. The value of correction factors comes from the calculated “correction” which is the opposite of “error”.

In this post, I have shared the following:

1. What is a Correction Factor in Calibration?
2. Important Use of a Correction Factor in Measurements
3. 4 ways to Apply Correction Factors In a Calibration Certificate
   • Applying directly the “correction” value
   • Using the Nearest Reported Correction Value in the Certificate
   • Averaging Between 2 Correction Factors
   • Linear Interpolation to Determine Any Value Between 2 points
4. Example of How to Apply the Correction Factor

Sometimes, we do not need to use a Correction Factor as long as the errors are very small or negligible and the tolerance limit is very wide, but as a good practice to follow and provide more accurate results, it is better to always implement its use.

Thank you for reading my post. If you like what you read, please share, subscribe and Buy Me A Coffee

Edwin